课堂实践性习题设计，促进学生思维提升
2023年10月7日，城厢四小课题组成员开展了课题“’学做一体’数学课堂培养小学生深度思维的实践研究”引领下的“学做一体”活动单课堂练习设计研讨，诣在研讨设计各年级促进学生思维能力提升的课堂综合实践类习题，引导学生在动手实践活动练习中产生深度思维进阶。
课题活动中，不仅课题组成员全员参与，同时邀请各年级数学教师共同参与，各教研组举例列举了相关练习设计及设计理念，集思广益，研讨氛围浓厚。练习举例如下：
低年级组：
1.分别求出每只小动物走了多长？
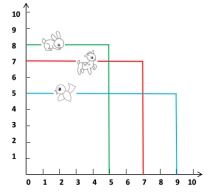
这是一年级上册教材数与代数的一道题，适合一年级学生学习了20以内进位加法后进行了练习。数与形结合的计算题给了学生计算的新鲜感，通过坐标图中的形与数、形与式之间的转换，培养学生的数感和空间观念，建立数与形之间的联系，通过选数组成算式的练习，既可以培养学生巩固20以内的进位加法计算，又可以培养学生有序思考的能力。在做本题时可以放手让学生观察、交流，引导他们发现每只小动物走了多长，其实就是将横着和竖着对应的数相加。
2.《燕几图》可以说是中国家具史上第一部组合家具的设计图，它由2张长方形大桌、2张长方形中桌、3张长方形小桌组成（图1），可以通过不同的拼搭组合成不同样式的桌子（图2），宴请客人，是“七巧板”的前身。
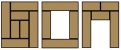
图1 图2
你也能设计一种桌子，尽可能宴请更多的客人吗？试着画一画，并在小组内介绍一下你的想法。
这是二年级综合实践“有趣的七巧板”中设计的联系，《燕几图》是七巧板的前身，通过阅读拓展课外知识的同时，通过动手拼一拼，画一画，感知数学的神奇，同时在各种变式中提高思维能力。
中年级组：
1.滨河公园有一条跑道，小军和小霞分别从跑道的两端同时出发，相向而行。如果小军每分钟走75米，小霞每分钟行65米,8分钟后两人相遇，那么这条跑道全长是（ ）米。
（先画图表示信息和问题，其次分析题目找出关键字词，找出数量关系，最后解答）
通过画图—审题、找数量关系—讲解算式的含义，这些有助于培养以下情况：一是培养用多种方法解题的习惯，学会常规方法，也要让非常规的列表、列举、画图、说理等方式成为常态解题方法，提升综合解决问题能力；二是培养化解学习弱项的良好习惯，针对存在的问题精选习题，开展专题练习，研究错题，化解错题；三是培养良好的答题习惯，审题细心，答题规范，完成后需检查。
经历解题的过程，训练学生学会利用数形结合的思想去解决问题，优化做题的策略，形成初步的模型意识，提升问题解决能力，促进思维发展。
2.苏教版数学课本四上第22页思考题改编
原题：小春在计算除法时，把除数72误写成了27，结果得到商26还余18。你能算出正确的结果吗？
新题：小马虎在计算一道除法算式时，将除数50末尾的0漏掉了，结果得到140余4，正确的结果是多少？
原题中，让学生根据被除数、除数、商、余数四者间等量关系反之推出被除数，学生基于将错就错思维，很容易联想到先求出被除数再用正确的除数求得结果，整体思路简单。众所周知，将错就错的意思是：明知道这件事情是错误的，还要继续地做下去。有的人看了题目可能要奇怪，严谨的数学计算，哪能知道错了还让它错下去？其实，这里的“将错就错”指的是：在数学计算中，告诉了错误的结果，需要求出正确的结果这时就需要根据错误的数据求出正确的结果。从而，让学生在错误与正确数据间拓展思考的维度。
高年级组：
1.问题1：用60块边长是1米的正方形地砖铺一块长方形的地，有多少种不同的铺法？得到的长方形的周长分别是多少？请一一列举出来，哪种情况下周长最短，你有说明发现？
问题2：我们常见的都是用长方形、正方形地砖来铺地，但其实用任意的凸四边形、五边形也能铺成一个平面，如图：
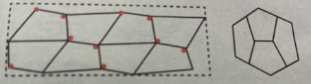
其实经过菜哈特和克什纳等数学家的研究，已经得出了13种用凸五边形平铺的方案了，你能画出几种呢？试着画一画（至少画一种）
通过本题，考查五年级学生对一一列举策略的掌握情况，是否能在面积一定的情况下发现长方形长、宽与周长之间的关系。同时由正方形拓展到凸四边形、五边形的平铺，尤其是凸五边形平铺的介绍，拓展了学生的课外知识量，在动笔画一画的过程中锻炼了操作能力、强化了对多边形内角和的应用，深化平面图形之间的联系。
2.巧克力是十分受同学们欢迎的，一家巧克力工厂要给新品巧克力设计长方体包装盒，现每颗巧克力是棱长2厘米的正方体，以12颗装一盒，怎样设计包装盒用材料（纸板）最少，包装盒表面积是多少平方分米？（接头处忽略不计）如果要在包装盒四周系上彩带装饰（如图），打结处需13厘米，共需彩带多少厘米？小卖部每个货架有3层，每层长6分米，宽4.9分米，高3.8分米，一个货架最多放多少盒这样的巧克力？
该题立足于生活实际问题，融合了长方体、正方体表面积计算、棱长计算、体积计算等多方面内容，同时又涉及了包装方式的多样性和最优方案的选择及单位的换算，学生在解决问题的过程中提升了思维能力，空间观念，引导学生用数学的眼光观察现实世界，用数学的思维思考现实世界的意识。
